Math 535a: Differential Geometry
USC Spring 2021

Instructor: Kyler Siegel (kyler.siegel@usc.edu)
Lectures: 11:00 - 11:50am (LA time), Mondays, Wednesdays, and Fridays via Zoom


Teaching assistant: Mark Ebert (markeber@usc.edu)

About.

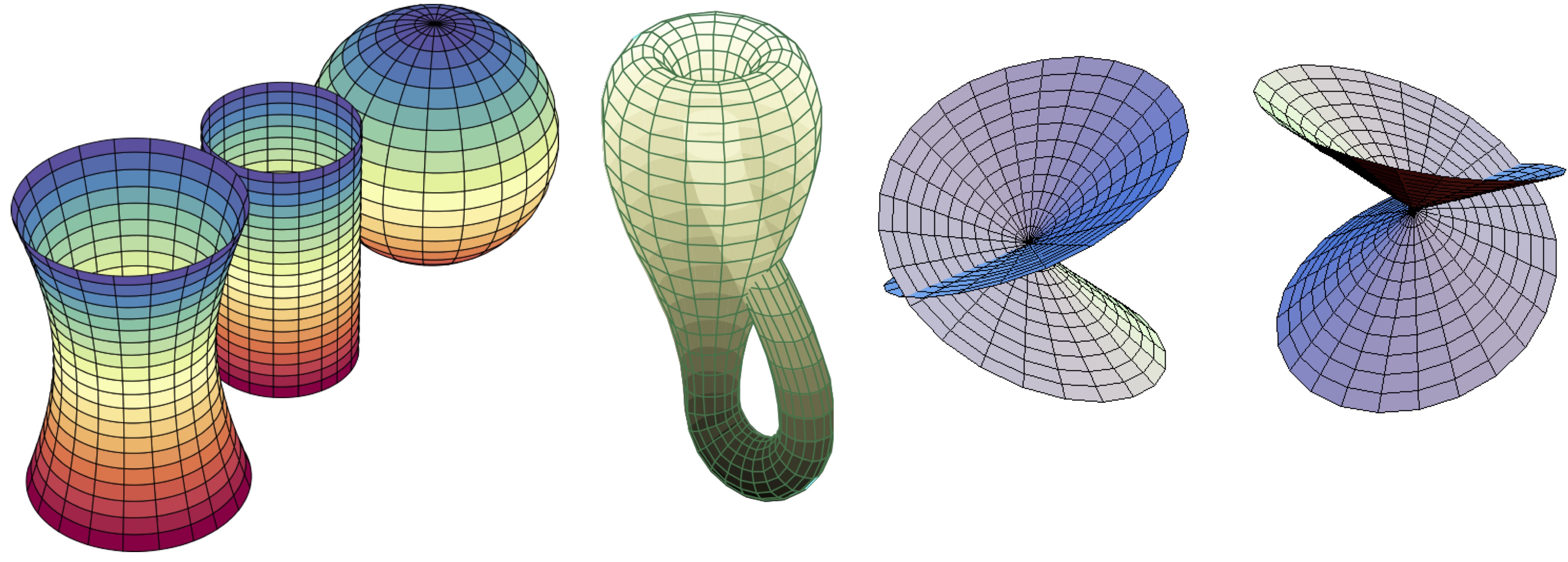
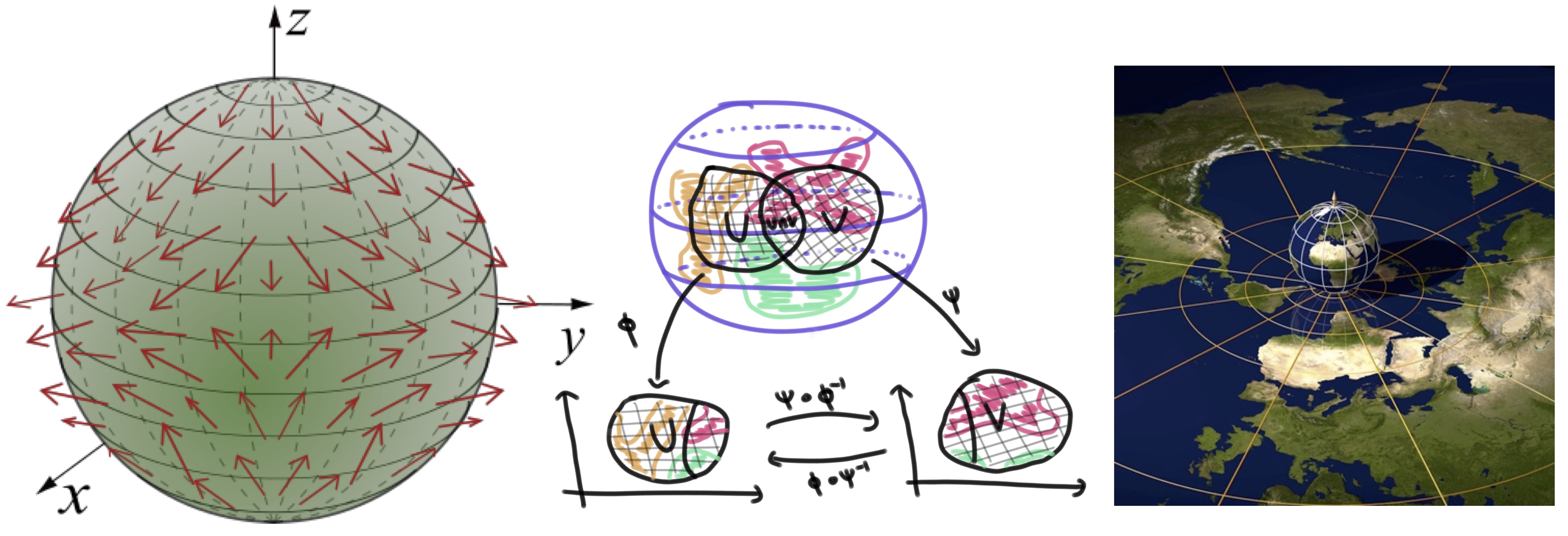
This course is an introduction to smooth manifolds. Roughly speaking, these are spaces which look locally like Euclidean space, but may have nontrivial global structure. The smooth structure allows us make sense of notions such as derivatives of maps, tangent vectors, embeddings, etc in this abstract setting. Although the basic definitions will appear at first glance somewhat abstruse, once set up properly the theory of smooth manifolds is remarkably rich, and plays a fundamental role in modern geometry.

Prerequisites.

We will assume familiarity with

  • basic point set topology: topological spaces, subspaces, quotient spaces, compactness, Hausdorffness, first and second countability, etc
  • basic linear algebra:determinants, dual spaces, etc
  • basic multivariable calculus and real analysis: partial and total derivatives, multivariable chain rule, multiple integrals, etc.

    If you are feeling a bit rusty on some of these, I recommend reading the appendix of Lee. You can also check out appendices A and D in Tu. Some knowledge of basic algebraic topology (especially homology and cohomology) will be also helpful, but we will not assume any prior exposure.

    Topics.

    Some of the topics we may cover over the course of the semester (time permitting) include:

  • topological manifolds, maximal atlases, smooth manifolds
  • examples of smooth manifolds
  • smooth maps between smooth manifolds
  • tangent vectors and the tangent bundle
  • vector fields and the Lie bracket
  • Lie groups and Lie algebras
  • vector bundles
  • covectors and the cotangent bundle, differentials of functions
  • submersions, immersions, embeddings
  • inverse function theorem and implicit function theorem
  • Lie group actions and quotient manifolds
  • Whitney's embedding and approximation theorems
  • tensors and multilinear algebra, differential forms
  • orientations, integration of differential forms
  • Stokes' theorem
  • de Rham cohomology and the re Rham theorem
  • integral curves and flows of vector fields
  • foliations and the Frobenius theorem
  • degree theory.

    Textbook.

  • Primary: Introduction to Smooth Manifolds (2nd edition) - John M. Lee
  • Secondary: An Introduction to Manifolds - Loring W. Tu

    • We will be primarily following Lee's book. This text is rather lengthy compared to others, but it is very well-organized and comprehensive. I suggest reading the relevant sections early (ideally in advance of the lectures) and often. You should think of the lectures as a guide to help develop your intuition about key concepts, with the primary textbook providing much fuller details and further elaborations. For an alternative perspective I recommend the secondary textbook by Tu, which provides a well-written and concise approach and covers similar material. Note that there are also numerous other popular introductory texts on smooth manifolds, and I encourage you to further utilize any references you find beneficial.


    Live lecture notes and recordings.

    The lectures and discussion sessions will be held via Zoom. The links and passwords can be found on Blackboard. Afterwards, Zoom recordings will appear on Blackboard. We strongly urge all students to attend the live lectures and discusssions if at all possible. Moreover, you are encouraged to actively participate by following along and asking and answering questions. We strongly request that you turn on your video feed in order to create a more responsive and social atmosphere.

    We understand that in some cases certain students will not be able to attend all live lectures due to time zone difficulties or other extenuating circumstances. In this case it is your responsibility to follow along with the recordings and other class materials.

    The lectures will primarily involve notes written in real time on an ipad. In addition to viewing lectures in Zoom via screen sharing, you will have the option of viewing the lecture notes in real time via this link. Some of you might find this useful if you wish to backreference something that happened earlier in the lecture. The completed past lecture notes will also be stored there. Note: the syncing is not instanteous, so you may sometimes need to refresh the document.

    Communication and discussion boards.

    USC has opted to use the messaging application Slack to facilitate communication between amongst students, and between students, instuctors, and TAs. Stay tuned for more details about our Slack workspace. You are encouraged to regularly post content (questions, answers, comments) on Slack. We will try to give responses as soon as possible.

    Problem sets.

    In addition to the lectures, there will be weekly problem sets. These will be listed on this website (see the schedule below) and will be handed in via Gradescope. Late homeworks will not be accepted without prior approval from the instructor or TA.

    Much of the course material will be developed in the problem sets. It is very important to do all of the problem sets to the best of your ability and to challenge yourself to solve the problems on your own, as this is the most effective way to absorb the material. We expect students to devote a significant amount of time to the problem sets.

    While working on the problem sets, you are allowed to consult or collaborate with your peers, as well as textbooks and the internet (apart from cheating websites such as Chegg or Cramster). However, you must write down attributions for any peer, textbook, website etc from which you took any significant ideas. Moreover, you must attempt all problems on your own and your submitted solutions must be written out originally and individually. Submissions which are copied or suspiciously similar are subject to being rejected and potential disciplinary action.

    Exams

    There will be one midterm exam and one final exam. These will most likely be 24 hour take home exams. The midterm will occur in early March and the final will occur in early May (precise dates TBA).

    Grading scheme.

    Homeworks: 40%, midterm exam: 25%, final exam: 35%.

    Office hours.

    For the time being, Kyler's office hours will be by appointment (in the future we may pick a fixed time if the class prefers to do it that way). If you wish to meet, please send Kyler an email with your availability and requested time, and he will try to accomodate as best he can. If you have any confusions / questions / comments / clarifications whatsover you are encouraged to come to office hours. Kyler will also typically stick around after the lecture so that is also a good time to ask additional questions.

    Tentative schedule

    Note: this schedule is tentative and will be continuously updated to adapt to the pace of the course. Please check back regularly for updates and problem set assignments.
    Date Material References Problem Set
    Friday 1/15/21 Topological manifolds and examples. Smooth atlases. Lee §1, Tu §1,§5. I also suggest reading the appendix of Lee and/or appendices A,D of Tu if you need a refresher. Problem set 1 (due Friday 1/22/21 by 11:59pm LA time).
    Monday 1/18/21 (MLK day - no class)
    Wednesday 1/20/21 Definition of smooth manifolds. Basic properties and examples. Lee §1.
    Friday 1/22/21 Smooth maps. Lee §2. Problem set 2 (due Monday 2/1/21 by 11:59pm LA time).
    Monday 1/25/21 More on smooth maps and diffeomorphisms. Partitions of unity. Lee §2.
    Wednesday 1/27/21 More on partitions of unity. Lee §2.
    Friday 1/29/21 Tangent spaces. Lee §3. Problem set 3 (due Monday 2/8/21 by 11:59pm LA time).
    Monday 2/1/21 More on tangent spaces. Diffentials of smooth maps and local coordinate representations. Lee §3.
    Wednesday 2/3/21 The chain rule. The tangent bundle. Lee §3.
    Friday 2/5/21 Maps of constant rank. Rank theorem and inverse function theorem. Lee §4. Problem set 4 (due Monday 2/15/21 by 11:59pm LA time).
    Monday 2/8/21 More on maps of constant rank. Proofs of the inverse function theorem and rank theorem. Lee §4.
    Wednesday 2/10/21 Finish proof of the rank theorem. Implicit function theorem. Global rank theorem. Lee §4.
    Friday 2/12/21 Submanifolds and regular level sets. Lee §5.
    Monday 2/15/21 (President's day - no class) More on submanifolds and regular level sets. Lee §5. Problem set 5 (due Monday 2/22/21 by 11:59pm LA time).
    Wednesday 2/17/21 More on submanifolds and regular level sets. Immersed submanifolds and examples. Lee §5.
    Friday 2/19/21 Null sets and Sard's theorem. Lee §6.
    Monday 2/22/21 Sard's theorem continued. Whitney's embedding and immersion theorems. Lee §6. Problem set 6 (due Monday 3/1/21 by 11:59pm LA time).
    Wednesday 2/24/21 Proof of Whitney's embedding theorem (weak version). Vector fields. Lee §6,8.
    Friday 2/26/21 More on vector fields. The Lie bracket of vector fields and naturality properties. Lee §8.
    Monday 3/1/21 More on vector fields and the Lie bracket. The Lie algebra of a Lie group. Lee §8, Lee §7.
    Wednesday 3/3/21 Properties and examples of Lie groups and Lie algebras. The Lie algebra of the general linear group. Lee §8, Lee §7.
    Friday 3/5/21 More on Lie groups and their Lie algebras. The orthogonal group. Lie group actions and quotient manifolds. The quotient manifold theorem. Lee §7, §21. Midterm exam: released 3/4/21 at 11:59pm PT on Gradescope, due 3/7/21 at 11:59pm PT.
    Monday 3/8/21 More on Lie group actions and the equivariant rank theorem. More on homogeneous spaces and examples. §21 (see also the Closed Subgroup Theorem in §20). Problem set 7 (due Wednesday 3/17/21 by 11:59pm LA time).
    Wednesday 3/10/21 More on homogeneous spaces. ODEs, integral curves, and flows of vector fields. Lee §9, §D. Midterm sample solutions.
    Friday 3/12/21 (wellness day - no class)
    Monday 3/15/21 More on integral curves and flows. Complete and incomplete vector fields. Lee §9 Problem set 8 (due Wednesday 3/24/21 by 11:59pm LA time).
    Wednesday 3/17/21 The flowout theorem and canonical form near regular points. The Lie derivative. Lee §9.
    Friday 3/19/21 More on the Lie derivative and commuting frames. Vector bundles. Lee §9, §10.
    Monday 3/22/21 More on vector bundles. §10.
    Wednesday 3/24/21 The contangent bundle. Covectors, dual bases, local trivializations, change of coordinates. §11. Problem set 9 (due Wednesday 3/31/21 by 11:59pm LA time).
    Friday 3/26/21 More on the cotangent bundle. Differential of a map, pullback of covectors. §11.
    Monday 3/29/21 More on the cotangent bundle. Line integrals. §11.
    Wednesday 3/31/21 More on line integrals. Closed, exact, and conservative covector fields. Fundamental theorem and the Poincare lemma. First de Rham cohomology group of a manifold §11. Problem set 10 (due Wednesday 4/7/21 by 11:59pm LA time).
    Friday 4/2/21 Multilinear algebra. §12.
    Monday 4/5/21 More multilinear algebra and tensor fields. §12.
    Wednesday 4/7/21 (wellness day - no class) Problem set 11 (due Wednesday 4/14/21 by 11:59pm LA time).
    Friday 4/9/21 More on symmetric tensor fields. Brief introduction to Riemannian metrics. Differential forms. §13, §14.
    Monday 4/12/21 More of the algebra of alternative tensors. The wedge product. Differential forms. §14.
    Wednesday 4/14/21 More on differential forms. Interior multiplication and pullback. §14. Problem set 12 (due Wednesday 4/21/21 by 11:59pm LA time).
    Friday 4/16/21 The exterior derivative. Coordinate definition and coordinate-free expression. Basic properties. §14,
    Monday 4/19/21 More on the exterior derivative. Cartan's magic formula. Introduce de Rham cohomology. Orientations. §14, §17, §15.
    Wednesday 4/21/21 The boundary orientation. Review of the multivariate (Riemann) integral. Change of coordinate formulas for integrals and top differential forms. §15, §C (multiple inegrals section), §16. Problem set 13 (due Friday 4/30/21 by 11:59pm LA time).
    Friday 4/23/21 More on integration on manifolds. Stokes' theorem. §16.
    Monday 4/26/21 More on Stokes' theorem. §16.
    Wednesday 4/28/21 Proof sketch of Stokes' theorem. Introduction to degree theory. §16, §17.
    Friday 4/30/21 (wellness day - no class)
    Final exam: Monday 5/3/21 Final exam sample solutions.
     
    Image sources: here.